Analyzing Unemployment Duration

Be data Driven or perish

jobs
survival curves
data Driven
modeling

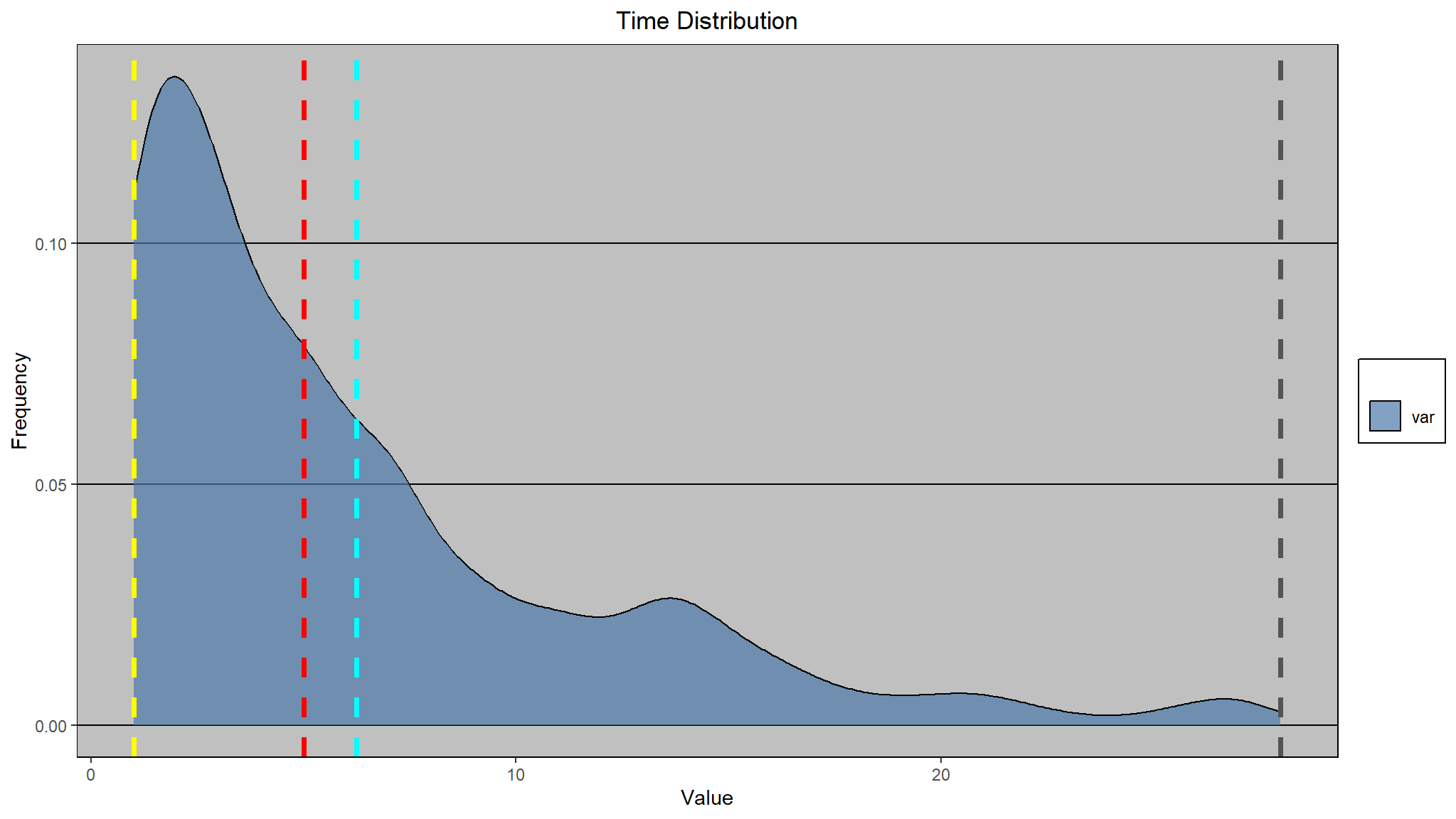
Explore survival functions for unemployment duration , we consider a cohort entering unemployment at the same time (first nonth) and we want to test if the survival rates are different for different age groups ,gender or unemployment insurance

Author

Bongani Ncube

Published

28 February 2024

Note

  • a closer look at survival analysis in unemployment

  • the dependent variable is made of two things

    • 0 implies a person has not found a job after 9 periods (censored)

  • ui stands for unemployment Insurance > the other variables are linked to that particular individual

Summary of the data at hand

spell ui event logwage married female age nonwhite
5 0 1 6.89568 1 0 41 0
13 1 1 5.28827 1 0 30 0
21 1 1 6.76734 0 0 36 0
3 1 1 5.97889 1 0 26 1
9 1 0 6.31536 0 0 22 0
11 1 0 6.85435 1 0 43 0

Recoding the data

out_new<-out_new |> 
  mutate(gender=ifelse(female==1,"Female","male")) |> 
  mutate(race=ifelse(nonwhite==1,"not white","white"))

Explanatory Analysis

Staggered Entry situation

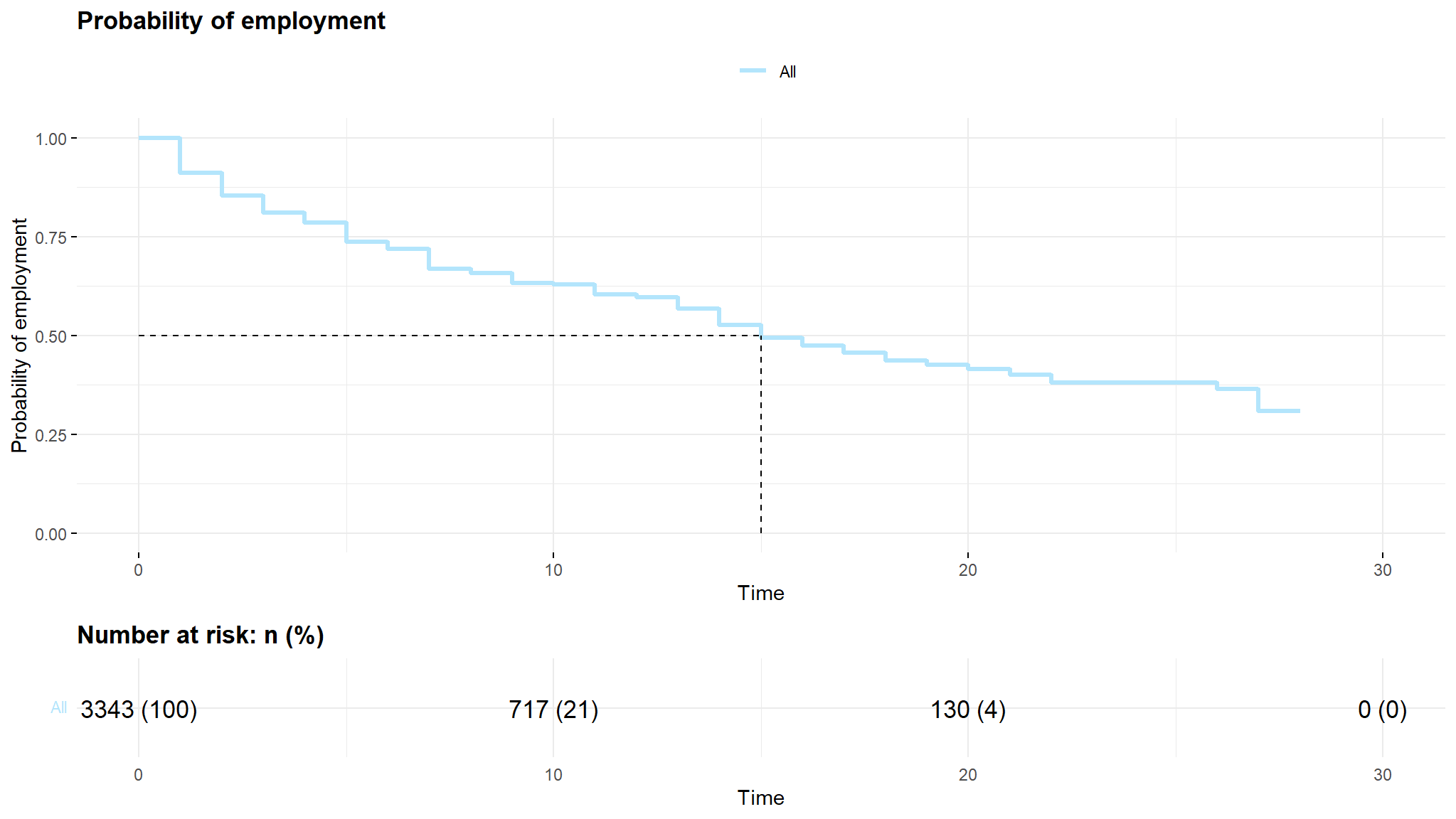
#> Call: survfit(formula = Surv(spell, event) ~ 1, data = out_new)
#> 
#>  time n.risk n.event survival std.err lower 95% CI upper 95% CI
#>     1   3343     294    0.912 0.00490        0.903        0.922
#>     2   2803     178    0.854 0.00622        0.842        0.866
#>     3   2321     119    0.810 0.00708        0.797        0.824
#>     4   1897      56    0.786 0.00756        0.772        0.801
#>     5   1676     104    0.738 0.00847        0.721        0.754
#>     6   1339      32    0.720 0.00882        0.703        0.737
#>     7   1196      85    0.669 0.00979        0.650        0.688
#>     8    933      15    0.658 0.01001        0.639        0.678
#>     9    848      33    0.632 0.01057        0.612        0.654
#>    10    717       3    0.630 0.01064        0.609        0.651
#>    11    659      26    0.605 0.01128        0.583        0.627
#>    12    556       7    0.597 0.01150        0.575        0.620
#>    13    509      25    0.568 0.01234        0.544        0.593
#>    14    415      30    0.527 0.01353        0.501        0.554
#>    15    311      19    0.495 0.01458        0.467        0.524
#>    16    252      10    0.475 0.01527        0.446        0.506
#>    17    201       8    0.456 0.01606        0.426        0.489
#>    18    169       7    0.437 0.01691        0.405        0.472
#>    19    149       4    0.426 0.01744        0.393        0.461
#>    20    130       3    0.416 0.01794        0.382        0.452
#>    21    109       4    0.400 0.01883        0.365        0.439
#>    22     82       4    0.381 0.02029        0.343        0.423
#>    26     48       2    0.365 0.02233        0.324        0.412
#>    27     33       5    0.310 0.02964        0.257        0.374
Note
  • looking at the survival curve ,note that it always starts at 1 and goes down in time
  • The median survival time is 14 periods
  • the output table shows that the probability of survival(= finding a job) in the first 2 months is 85.4% (84.2-84.66 CI) , the probability of survival gradually decreases with time in the 28 months and almost approaching zero.

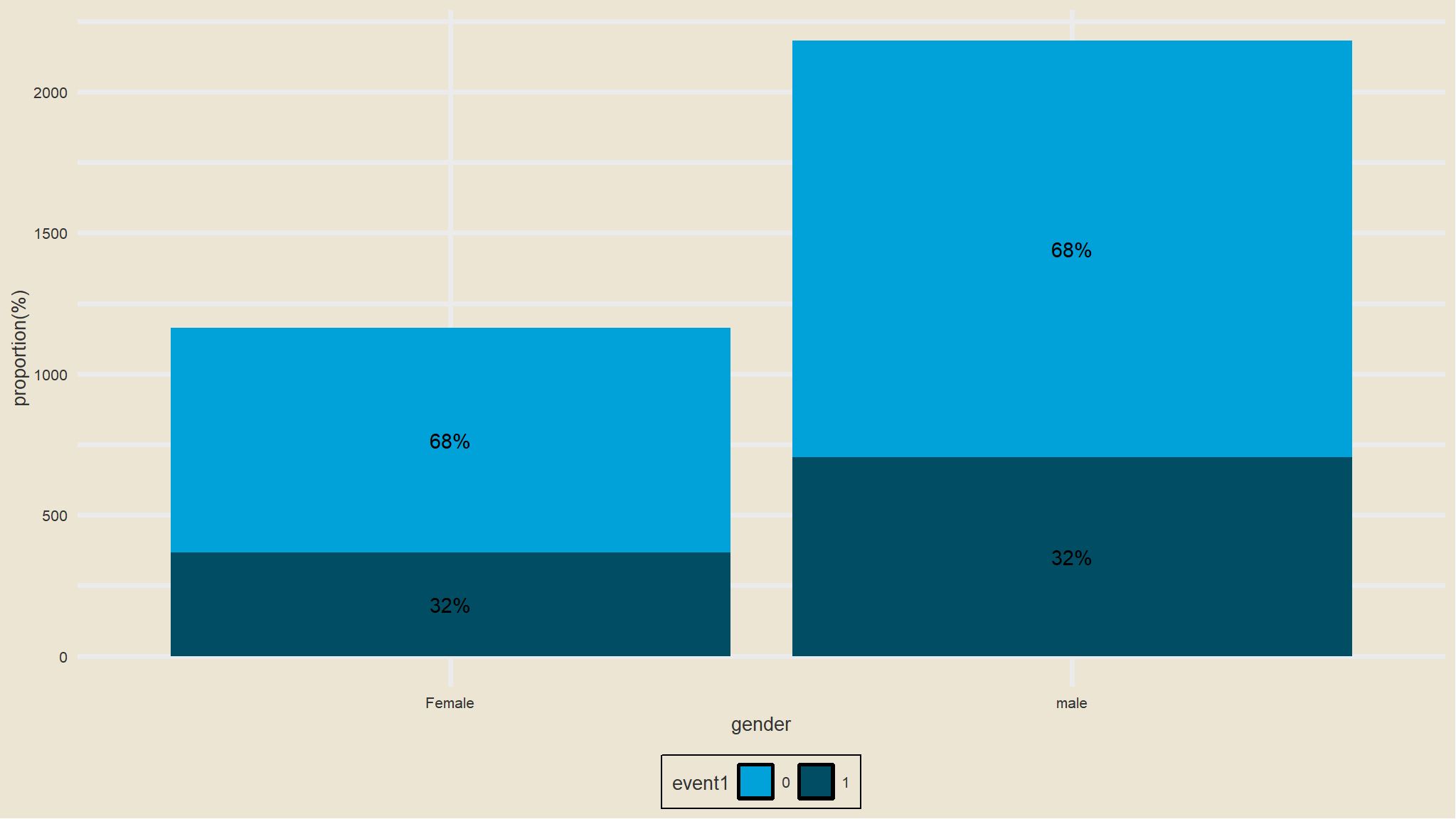
Summary by gender

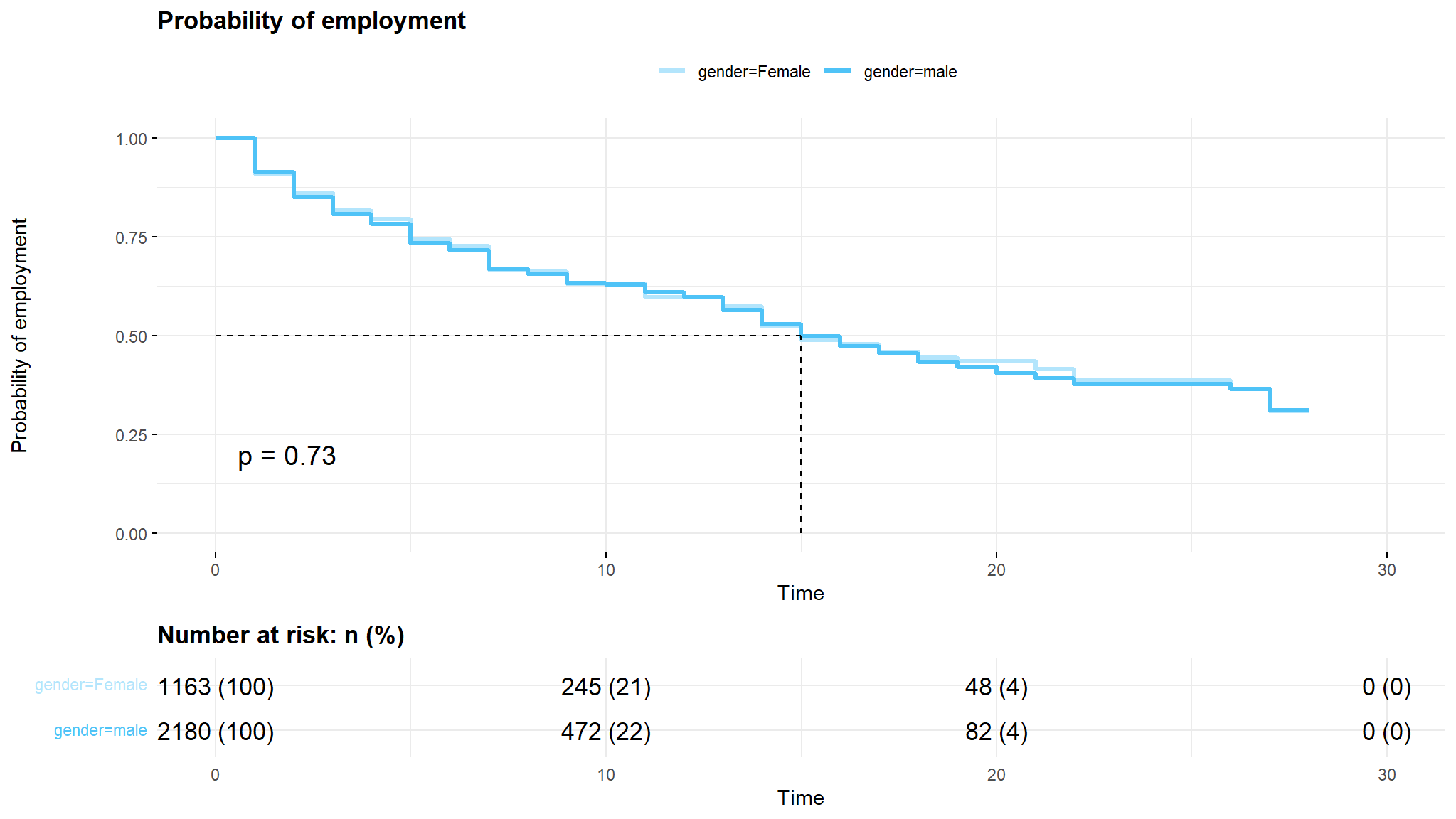
Note
  • there are minor differences in the survival times (time to get employed) between males and females

Summary by Unemployment Insurance

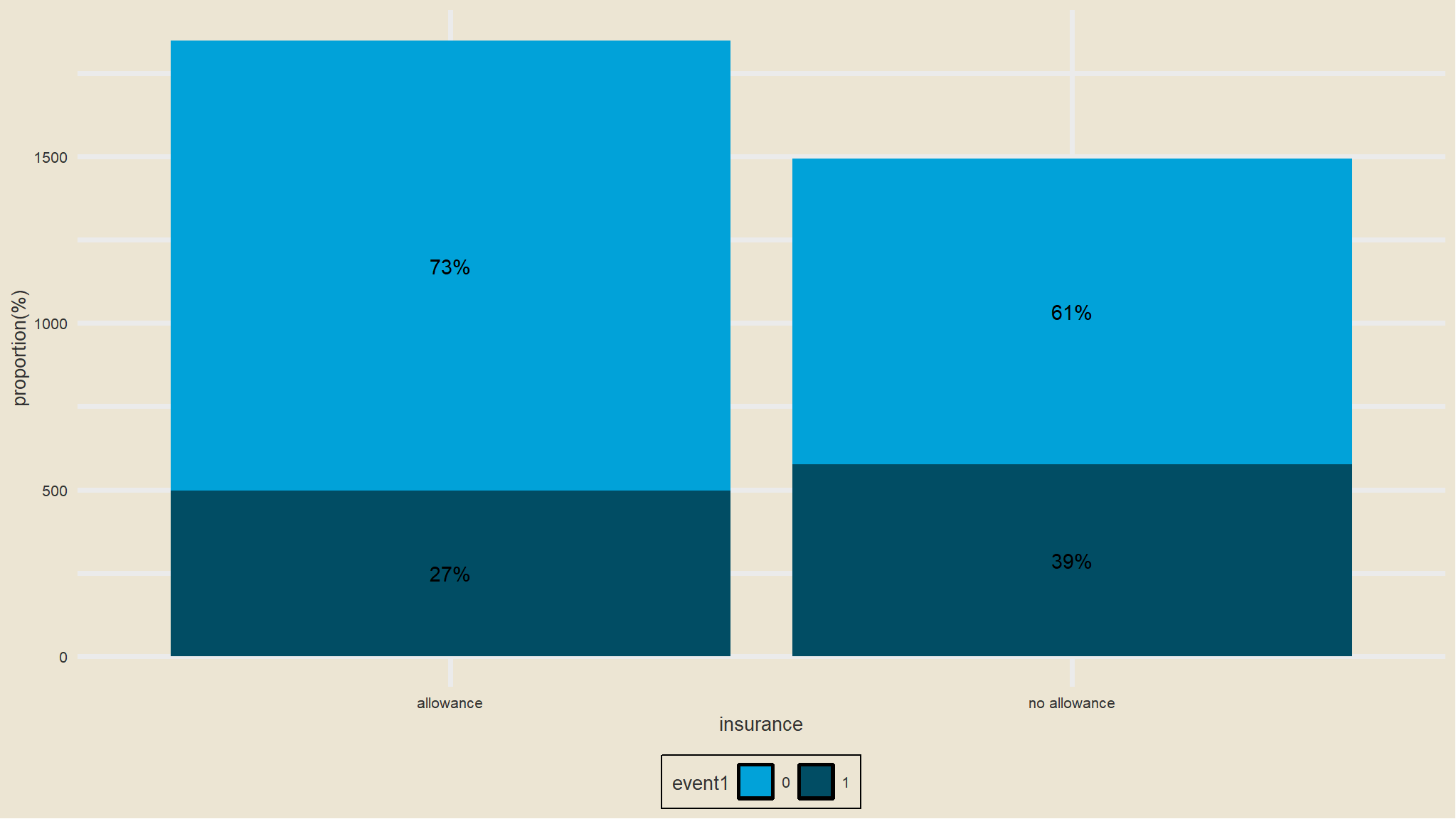
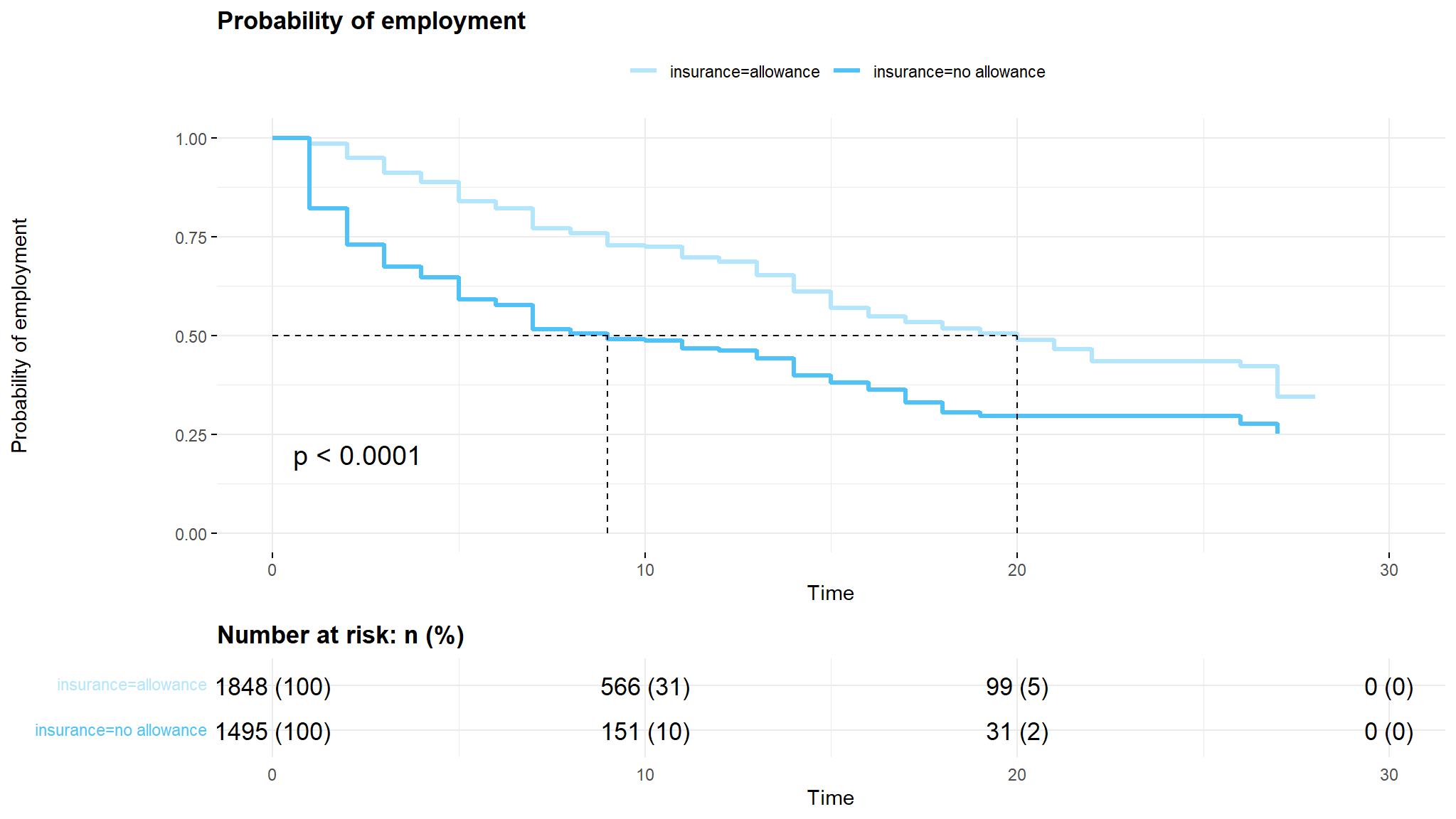
comment
  • after half of the time intervals i.e (10 and 15) we see that those having unemployment benefit have about 75% survival while the other group has 50% survival this means that 75% of those taking allowance are still not employed after half of the time.
  • it can be noted from the log rank that the survival times between these groups is significantly different

Exploring Age

  • distribution of age
#> Minimum: 20.00
#> Mean: 35.44
#> Median: 34.00
#> Mode: 27.00
#> Maximum: 61.00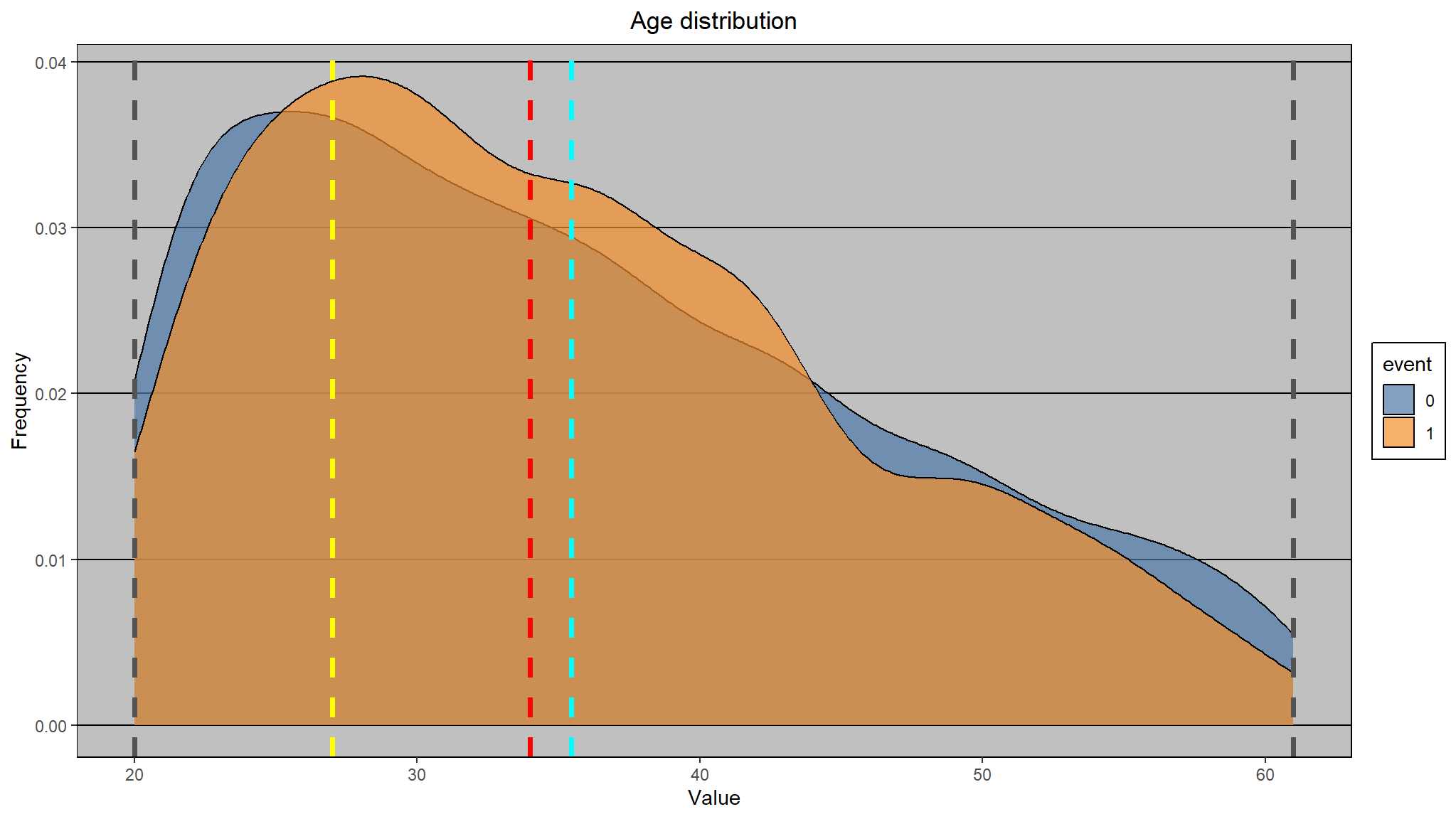

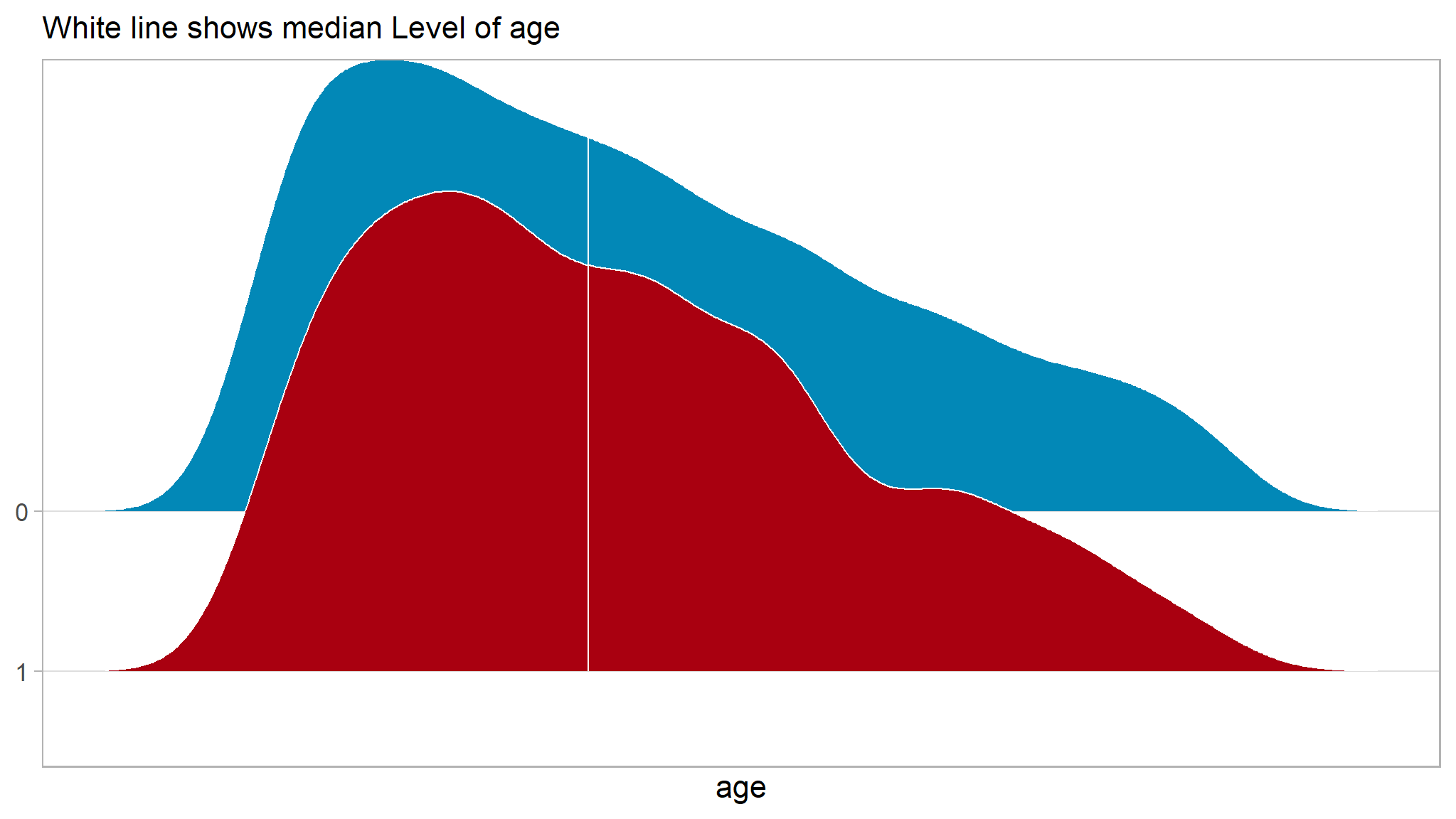
Put age into categories

  • we attempt to determine weighted (0%, 2.5%,10%,25%,50%,75%,90%,97.5%) quantiles of age and categorize the data in that order.
bins <- c(0,0.025,0.10,0.25,0.5,0.75,0.9,0.975,1)
split.Age <- wtd.quantile(out_new$age,probs=bins)
split.Age
#>    0%  2.5%   10%   25%   50%   75%   90% 97.5%  100% 
#>    20    21    23    27    34    43    52    58    61
Note

the data above simply shows:

  • minimum of 20 years of age
  • lower quartile of 27 years implying that about 25% are below the age of 27
  • median age of 34 years implying that about 50% are below the age of 34
  • upper quartile of 43 years
  • maximum of 61
  • categorize age into the above bins
level <- c(20,21,23,27,34,43,52,58,61)
out_new<-out_new |> 
  mutate(age_cat=cut(age,level,labels=c("20-21","22-23","24-27","28-34",
                                          "35-43","44-52","53-58","59-61")))

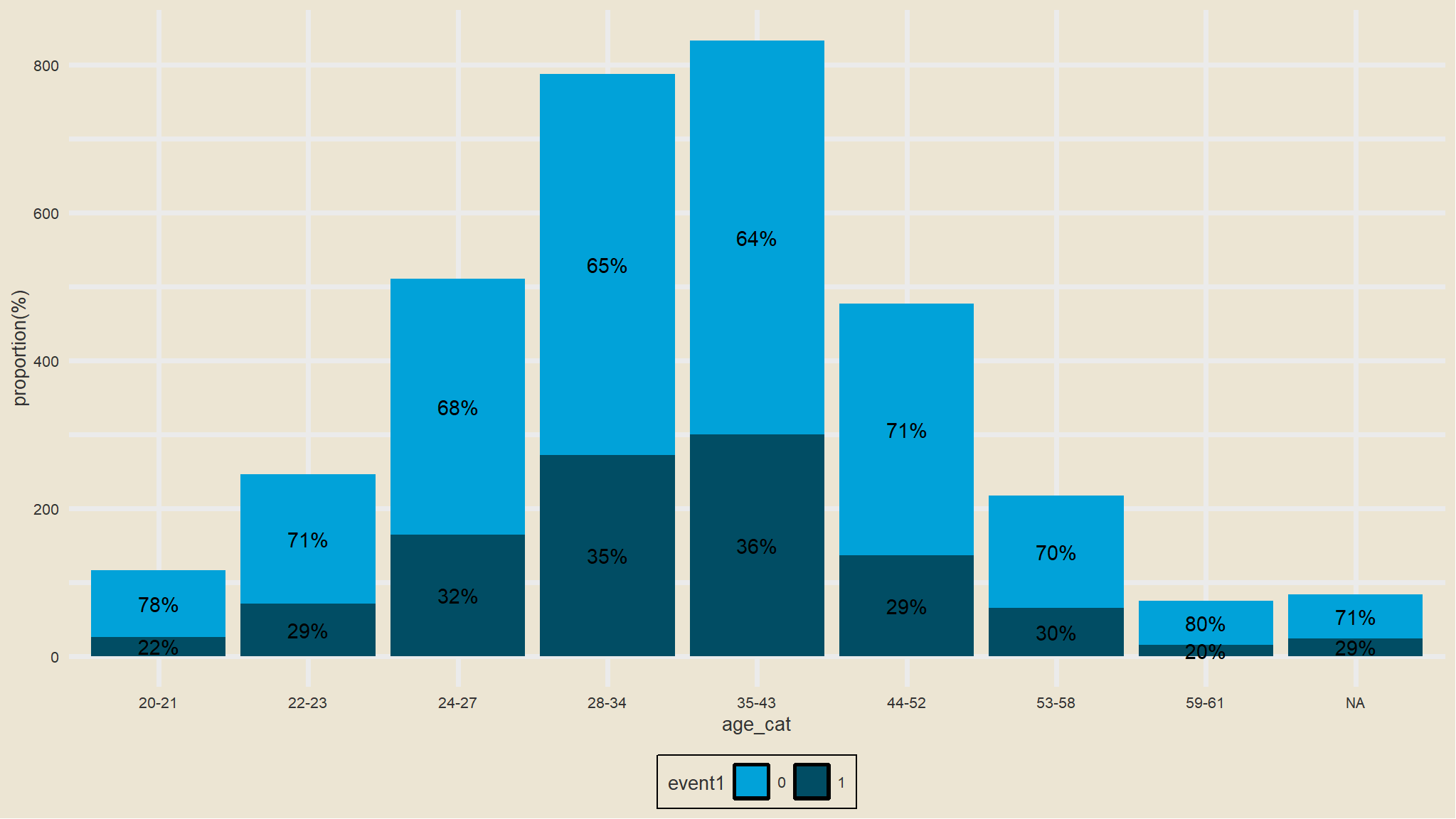
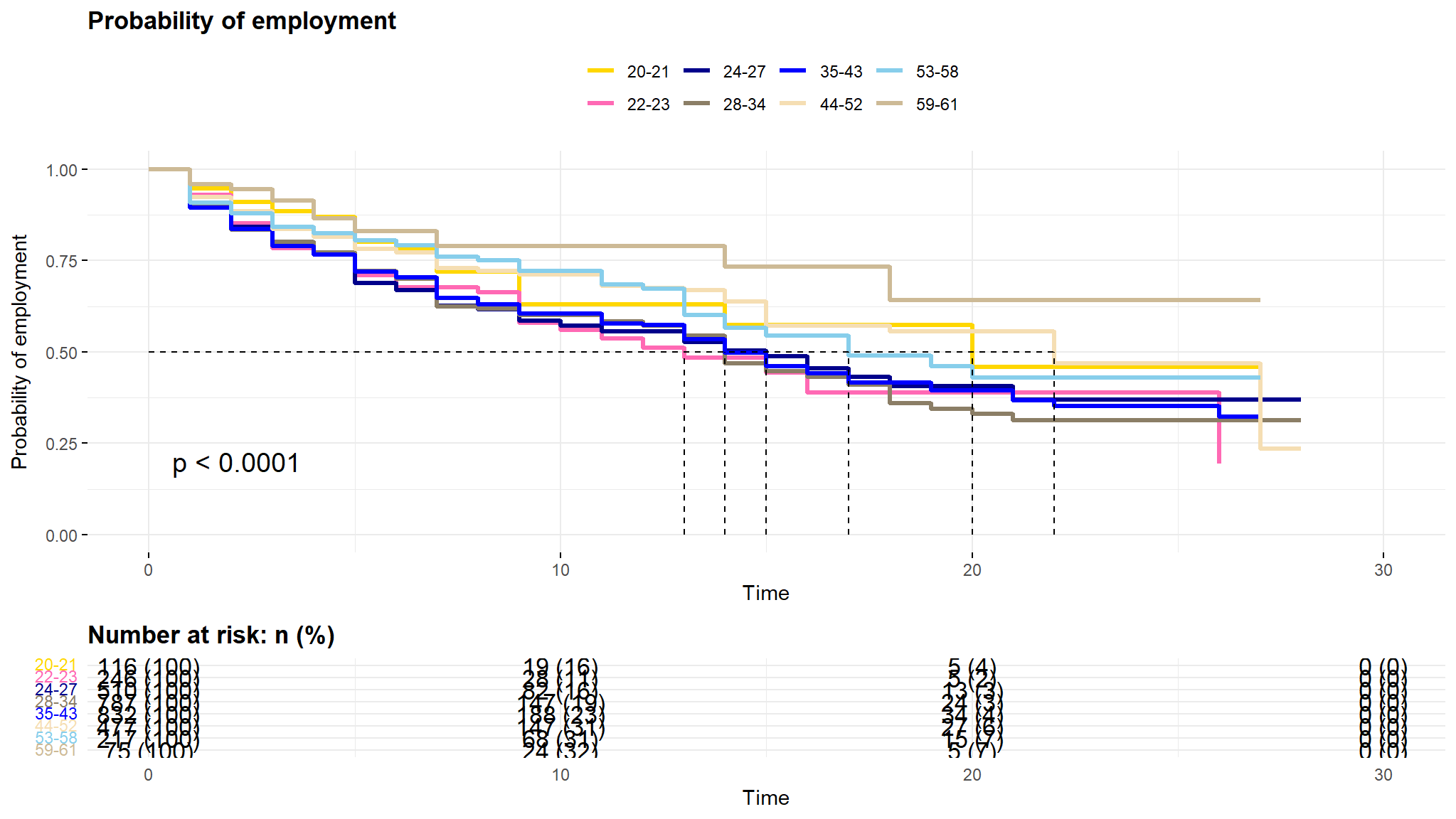
comment
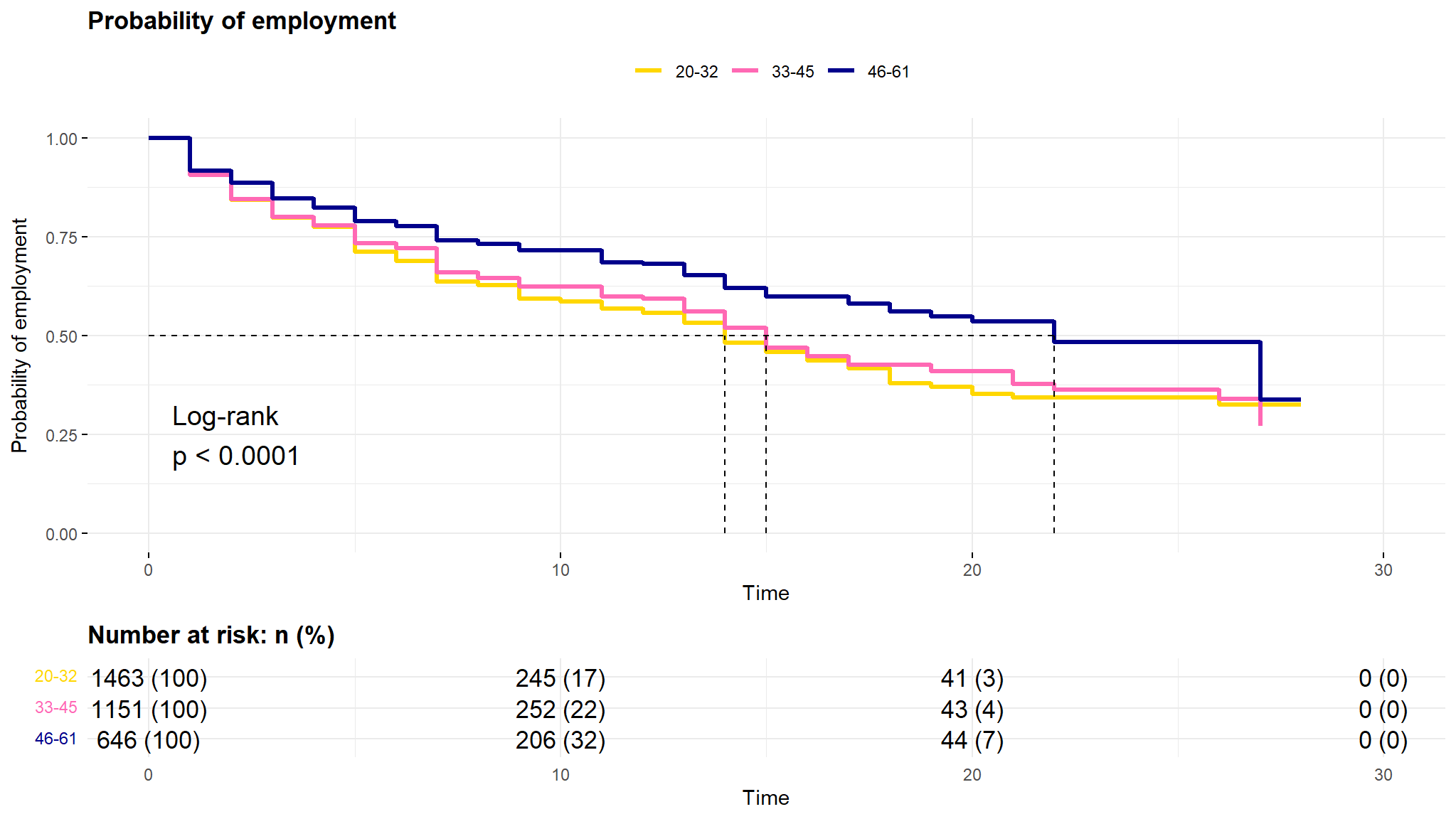
  • we notice a strong difference in these curves starting at period 10 and an almost inversion of them at period 20
  • its easy and obvious to note that those in the upper age groups stay unemployment for a longer time implying that it is hard for the age groups 44-52 and 53-61 to get a job as compared to the lower age groups
  • those in the lower age groups get employed much faster (much easier for them to get employed)

try another binning

level <- c(20,32,45,61)
out_new <- out_new |> 
  mutate(age_cat_new_level = cut(age, level, labels = c("20-32", "33-45", "46-61")))

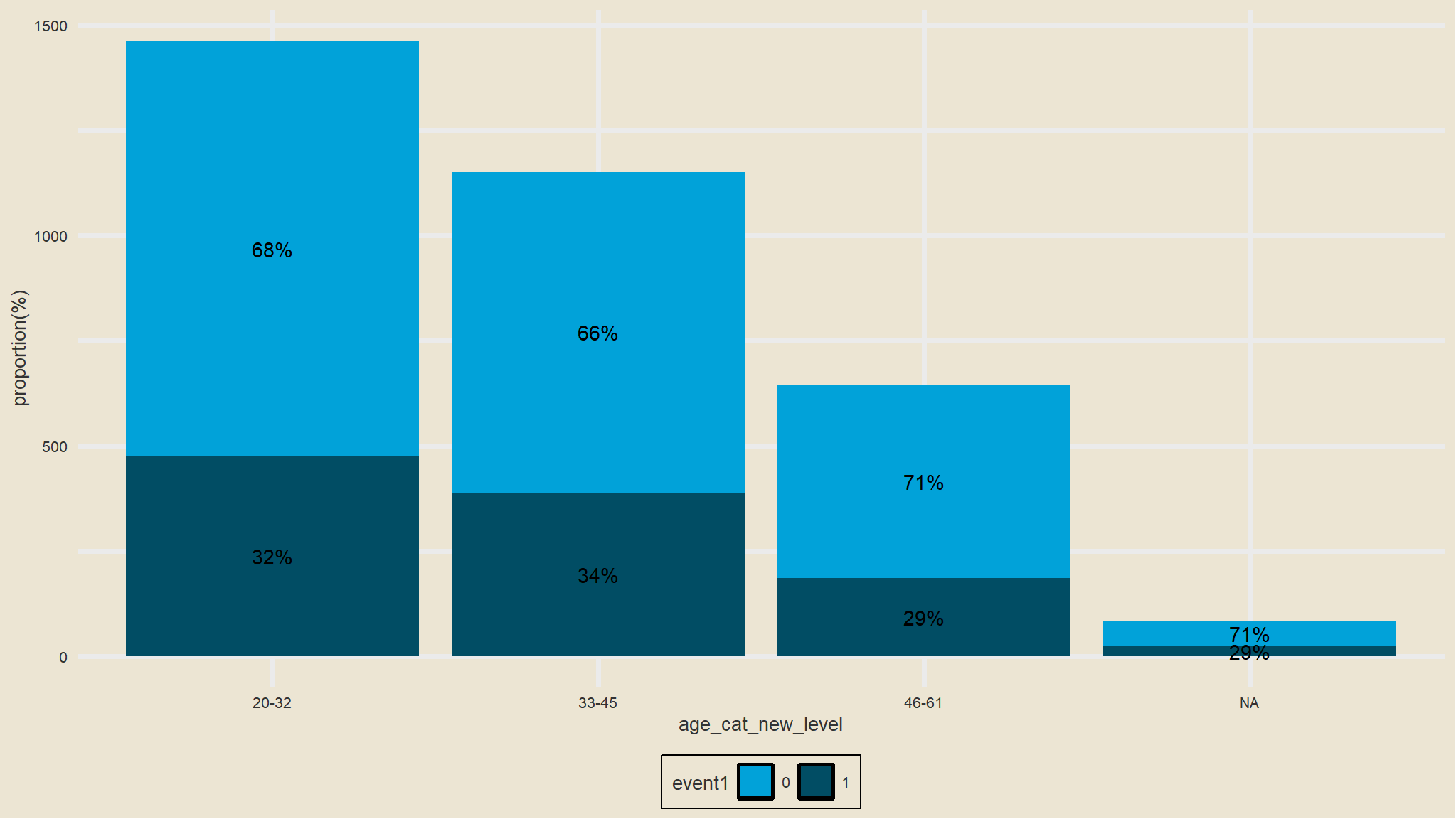
comment
  • the observation is the same as from the previous age bins

Exponential survival probability

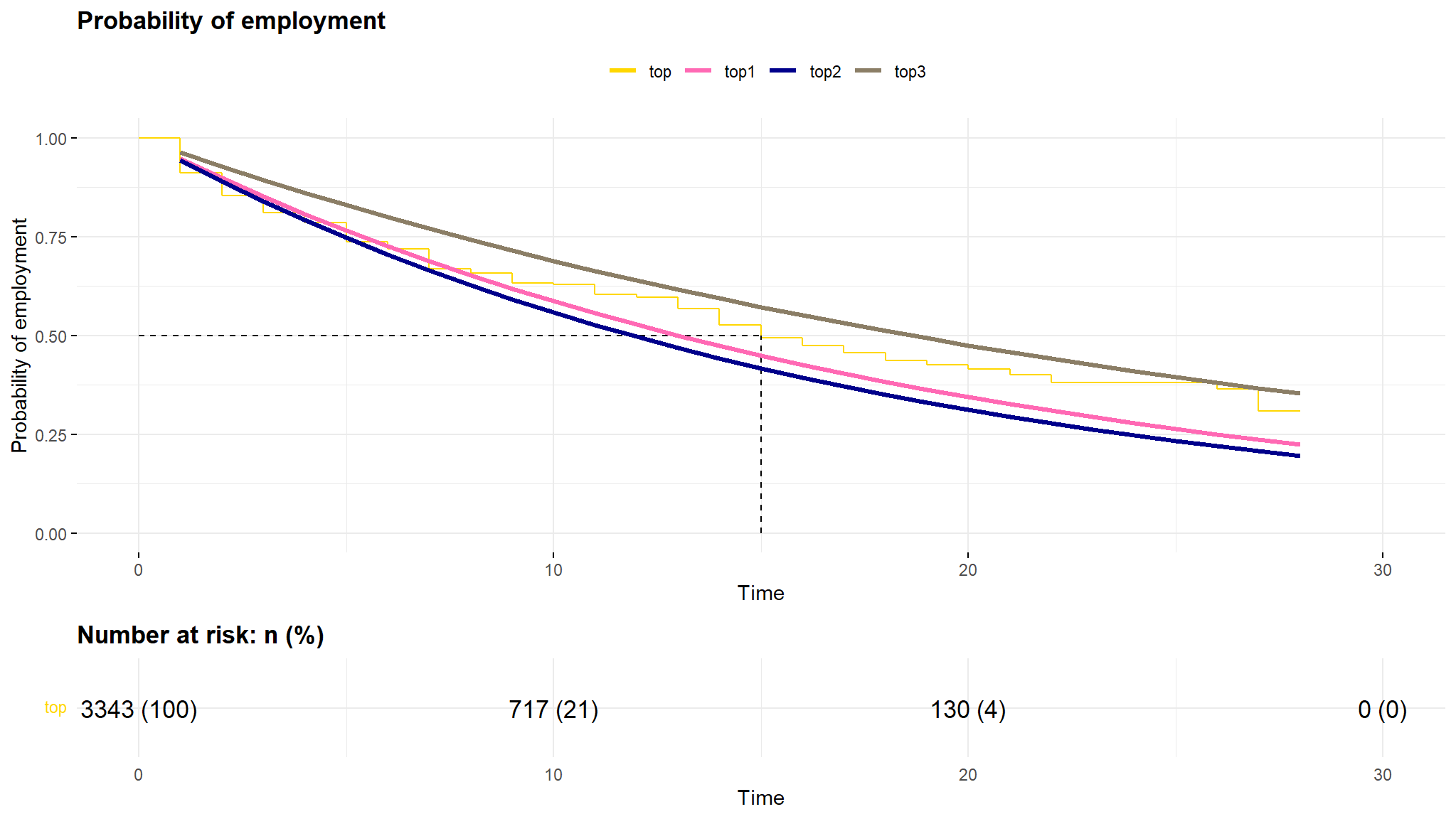
Cox proportional Hazard

  • assume age is not categorized
Characteristic HR1 95% CI1 p-value
logwage 1.69 1.50, 1.90 <0.001
gender


    Female — —
    male 0.86 0.75, 0.98 0.028
age 0.99 0.98, 1.0 <0.001
insurance


    allowance — —
    no allowance 2.79 2.46, 3.16 <0.001
1 HR = Hazard Ratio, CI = Confidence Interval
Comments
  • holding all other covariates constant ,increase in age reduces the hazard of employment by 0.98
  • an increase in log wage increases the hazard of employment by 0.48
  • man have a decreased hazard of employement as compared to women
  • what if age is categorised
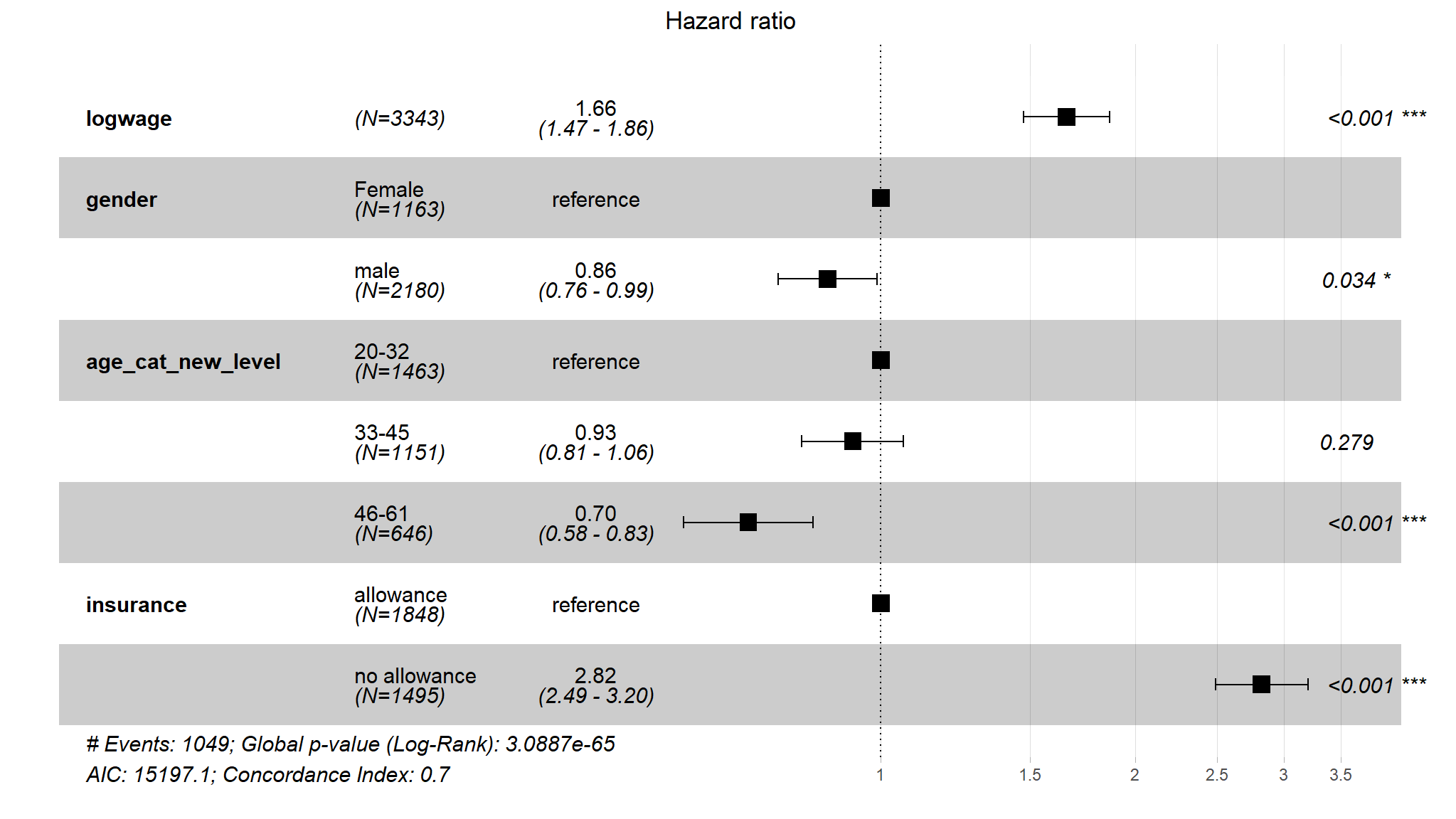
Characteristic HR1 95% CI1 p-value
logwage 1.66 1.47, 1.86 <0.001
gender


    Female — —
    male 0.86 0.76, 0.99 0.034
age_cat_new_level


    20-32 — —
    33-45 0.93 0.81, 1.06 0.3
    46-61 0.70 0.58, 0.83 <0.001
insurance


    allowance — —
    no allowance 2.82 2.49, 3.20 <0.001
1 HR = Hazard Ratio, CI = Confidence Interval
Note
  • the results are almost the same , noting that the age groups 33-45 and 46-61 have decreased hazards of employment as compared to the 20-32 age group.

which model is better

AIC(cox_m,cox_m1)
#>        df      AIC
#> cox_m   5 15197.10
#> cox_m1  4 15593.82
Note
  • a model with age categorized perform better with a lower Akaike Information Criterion of 15451.18

Visualise the results

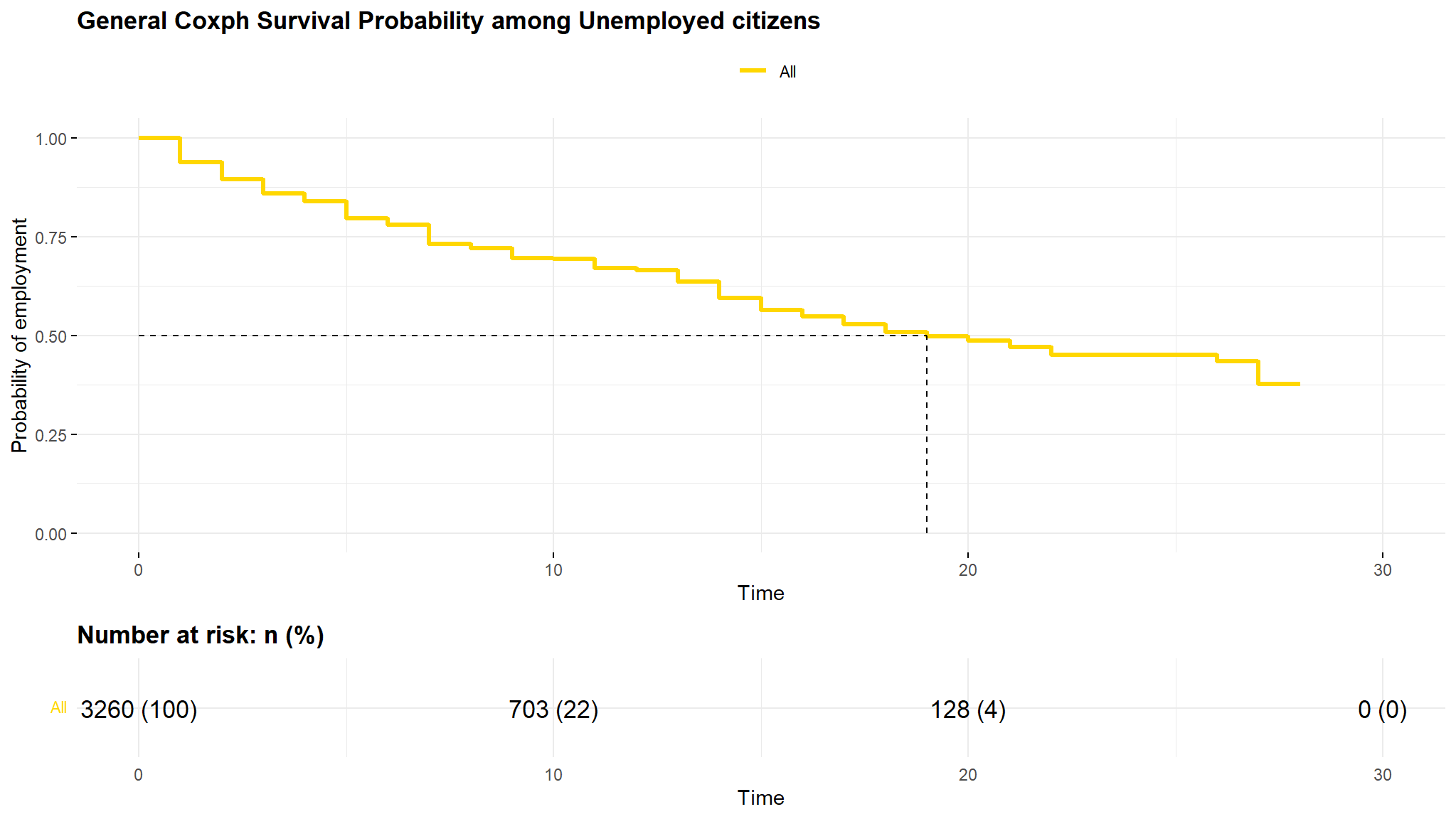
Conclusions
  • there is no strong differences between women and men concerning their unemployment duration
  • the higher age groups have a higher probability of remaining unemployed , i think it is harder for them to adapt to the new labor market
  • lastly as seen from the kaplan Meier Curve , those without insurance allowance have an increased hazard of employment as compared to the other group.